王新  張華兵

中國石油管道科技研究中心/中國石油天然氣集團公司油氣管道輸送國家工程實驗室 

摘要：《油氣管道完整性管理規范》給出了輸氣管道的潛在影響半徑計算公式，該公式對計算過程進行了大量簡化和假設，得出了基于管道管徑與壓力的簡化公式，在輸氣管道高后果區識別中得到廣泛應用。通過對該簡化公式存在的問題進行分析，表明簡化公式在泄漏衰減因子、泄漏系數、熱輻射計算模型、火災熱輻射閾值等方面的取值，都會導致計算結果與真實事故影響半徑的偏差。并通過與油氣管道失效后果定量評價軟件RiskInsight進行實例對比分析，結果表明：簡化公式計算的潛在影響半徑結果偏小，管道管理者仍可以采用該公式進行快速計算，但需要注意該公式的前提假設。當需要更加嚴謹的計算結果時，應該采用專業軟件。

關鍵詞：輸氣管道；噴射火；潛在影響半徑；簡化公式；RiskInsight 

輸氣管道一旦泄漏發生火災爆炸，將嚴重威脅周邊人員的人身安全。輸氣管道事故對周邊人員的影響范圍，即輸氣管道潛在影響半徑的計算一直是重要的技術問題，在GB 32167-2015《油氣管道完整性管理規范》中，給出了基于管徑與壓力的輸氣管道潛在影響半徑計算公式，即下文中的公式（5）。該公式最早出自加拿大C-FER 技術公司的研究報告^[1]，后來寫入了ASME B31.8S標準《輸氣管道系統完整性管理》，國內將其采標為SY/T 6621而廣為大家所知^[2]。

計算輸氣管道潛在影響半徑需要考慮諸多因素，計算過程十分復雜，需要專業軟件和專業技術人員才能完成，目前較為知名的軟件有荷蘭應用科學研究院（TNO）開發的Effect軟件和DNV開發的SAFETI^TM軟件^[3]；國內中國安全生產科學研究院開發的CASST-QRA軟件^[4]；中國石油管道科技研究中心開發了油氣管道失效后果定量評價軟件RiskInsight，也進行了大量應用，并通過了與真實管道事故的對比驗證^[5]。但為了讓管道管理者快速簡便進行計算，ASME B31.8S對該計算過程進行了大量簡化，并做了很多假設，得到了輸氣管道潛在影響半徑簡化計算公式。本文將討論嚴謹的輸氣管道潛在影響半徑計算與該簡化公式之間的差異。

1  輸氣管道的潛在影響半徑簡化公式

1.1  簡化公式的主要設定

計算輸氣管道潛在影響半徑過程中需要確定幾個重要問題。

（1）泄漏速率：簡化公式中泄漏速率為輸氣管道破裂時的泄漏速率，主要由管道管徑和管道壓力確定，泄漏速率采用峰值泄漏速率與泄漏衰減因子的乘積；

（2）熱輻射模型：假設噴射火焰熱源為一系列位于射流軸線上的點熱源，采用點源模型計算火災熱輻射；

（3）熱輻射閾值：采用15.8 kW/m²，計算結果為噴射火造成1%概率死亡的潛在影響半徑。

1.2  計算氣體泄漏速率

輸氣管道在發生破裂時，由于管道內壓力的不斷降低，天然氣的泄漏速率隨時間不斷減小。在計算噴射火熱輻射影響時，ASME B31.8S采用管道泄漏過程中的當量泄漏速率來表征泄漏速率，當量泄漏速率為峰值泄漏速率乘以泄漏速率衰減因子^[3]：

                           （1）

                                                     （2）

式中，當量泄漏速率，kg/s；釋放衰減因子；為峰值泄漏速率，kg/s；泄漏系數；管道直徑，m；管道運行壓力，Pa；流動因子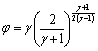；氣體聲速，；氣體比熱比，對于甲烷取1.306；為理想氣體常數J/(kg·mol)/K；為氣體溫度，K；為氣體摩爾質量。

1.3  噴射火熱輻射模型

ASME B31.8S在計算噴射火熱輻射時采用點源模型，點源模型假設火焰熱源為一系列位于射流軸線上的點熱源，并保守認為總熱輻射通量為每個點熱源熱輻射通量之和^[6]：

                                 （3）

式中，為熱輻射通量，kW/m²；為燃燒系數，對于噴射火取0.35；X_g為輻射系數，取0.2；Q為氣體泄漏質量流率，kg/s；H_c為燃燒熱，對于甲烷取50 000 kJ/kg

1.4  熱輻射閾值

ASME B31.8S中潛在影響半徑為人員在噴射火熱輻射影響下1%概率死亡的半徑，所取的熱輻射閾值為15.8  kW/m^2 [7]，代入式（3）可得：

                                          （4）

代入各項參數，可得潛在影響半徑為：

                               （5）

公式（5）即為目前廣泛使用的簡化公式（以下皆稱簡化公式）。

2  簡化公式的幾個問題

2.1  泄漏衰減因子的取值

輸氣管道在發生破裂后，管道內壓力不斷降低，天然氣的泄漏速率隨時間不斷減小，泄漏速率變化趨勢如圖1所示。

 

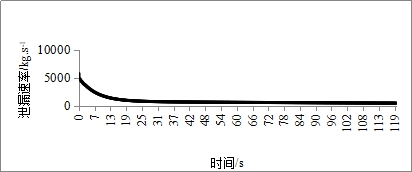
圖1 管徑710 mm壓力8 MPa的天然氣管道破裂后泄漏速率變化趨勢

如圖1所示，管道泄漏后泄漏速率是隨時間不斷變化的，在計算噴射火熱輻射影響時，簡化公式采用管道泄漏過程中的當量泄漏速率來表征泄漏速率。從式3可以看出，潛在影響半徑與當量泄漏速率密切相關，而當量泄漏速率很大程度上取決于泄漏速率衰減因子（公式1），因此泄漏衰減因子的取值對潛在影響半徑計算結果的準確性有著極大影響。荷蘭應用科學研究院（TNO）對輸氣管道泄漏速率衰減規律進行了一系列實驗研究，認為不同管道的泄漏速率衰減因子在0.20-0.50之間^[8]。英國HSE將管道泄漏衰減因子取為0.25^[9]，而簡化公式在計算潛在影響半徑時，將泄漏速率衰減因子保守取為0.33^[3]。即簡化公式認為峰值泄漏速率降到三分之一時，泄漏速率趨于穩定。然而泄漏速率衰減因子的取值與泄漏點位置、管道直徑、管道泄漏點處的壓力等因素密切有關^[10]，不同管道泄漏工況的泄漏衰減因子的取值應該有所區別，將泄漏衰減因子統一取值為0.33，會造成不同泄漏工況潛在影響半徑計算結果的誤差。

高壓天然氣管道在發生泄漏時往往會在很短時間之內引發噴射火，人員對于火災熱輻射的反應時間也往往小于30 s^[11]，因此噴射火熱輻射危害往往發生在發生噴射火的初始階段，噴射火的熱輻射危害與管道初始泄漏速率和質量密切相關。為了更準確的計算噴射火熱輻射危害，RiskInsight軟件中關于當量泄漏速率的計算方法，采用荷蘭應用科學研究院紫皮書中的方法，這種方法按照管道泄漏質量將管道泄漏過程分為5個階段，每個階段的泄漏質量M_eff為全部泄漏質量M_all的20%，計算噴射火采用的當量泄漏速率Q_eff為第一個泄漏階段的平均泄漏速率，這種當量泄漏速率的計算方法要更為科學合理^[12]。圖2為不同管徑時簡化公式計算的當量泄漏速率與RiskInsight軟件計算的當量泄漏速率比較，從圖中可以看出簡化公式計算的當量泄漏速率要比RiskInsight軟件當量泄漏速率小，這樣可能導致簡化公式計算結果偏小。

 

 

圖 2  不同管徑下簡化公式與RiskInsight軟件計算的當量泄漏速率比較

2.2   泄漏系數值的選取

天然氣從管道泄漏孔口或狹縫中向外泄漏的過程中，在泄漏孔口處發生縮頸現象，即實際流動面積小于泄漏口面積，使得理論流量與實際流量有差異，因此要引入泄漏系數予以修正。泄漏系數值直接影響氣體泄漏速率的計算。一般而言,泄漏系數的取值范圍在0.6—1.0之間。按泄漏孔的形狀可分：圓形孔值為1.00；三角孔值為0.95；長形孔值0.90^[13]。一般管道發生破裂時，泄漏系數取值為1.00，而簡化公式取0.62，最終可能使得管道潛在影響半徑的計算結果偏小。

2.3  熱輻射計算模型的選擇

目前，噴射火熱輻射的數學計算模型主要有兩種：點源模型和固體火焰模型（Thornton模型），簡化公式選用點源模型。點源模型假設火焰熱源為一系列位于射流軸線上的點熱源，并保守認為總熱輻射通量為每個點熱源熱輻射通量之和，模擬計算噴射火時過于簡化火焰形狀，導致計算結果準確性不高^[14]。而Thornton模型從火焰形狀的角度出發，假定噴射火形狀為平截頭圓錐形，符合噴射火長度較長的特點，并且該模型經過風洞和場地實驗驗證，計算結果較為準確^[15]。圖3為同樣工況時固體火焰模型與點源模型熱輻射計算結果對比圖，從圖中可以看出點源模型和Thornton模型計算結果存在差異，尤其是距離泄漏口較近時，點源模型的計算結果過大，可能導致最終簡化公式的計算結果偏大。

 

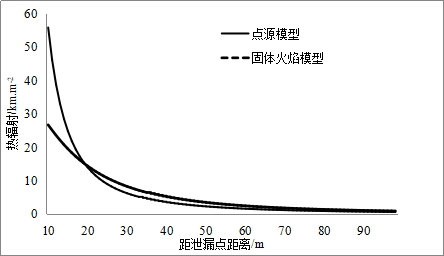
圖 3  相同工況時點源模型和固體火焰模型計算結果比較

2.4  火災熱輻射閾值的選取

簡化公式中潛在影響半徑為人員在噴射火熱輻射影響下1%概率死亡的半徑，所取的熱輻射閾值為15.8 kW/m²。而通常火災熱輻射的安全距離（人員基本不受影響，有輕微灼熱感）計算采用的熱輻射閾值為4 kW/m²，導致人員灼熱死亡半徑熱輻射閾值為37.5 kW/m^2 [16]。因此簡化公式中潛在影響半徑既不是天然氣管道破裂時的安全距離，也不是死亡半徑，而是一個中間值。這種情況下，人員暴露會被一定程度燒傷。所以簡化公式計算的管道潛在影響半徑會比真正的輸氣管道事故人員死亡半徑大，比人員基本不受影響的半徑小。

2.5  爆炸沖擊波影響分析

輸氣管道泄漏后，如果沒有立即被點燃，泄漏天然氣會在空氣中擴散，極易與周圍空氣混合形成爆炸性蒸氣云，如果遇到引火源將會爆炸，在輸氣管道泄漏后果分析中，蒸氣云爆炸沖擊波的潛在影響半徑較噴射火要大^[17]，但由于蒸氣云爆炸需要在特定的氣象及地形條件下形成，其發生概率較噴射火要小，因此一般計算輸氣管道潛在影響半徑時，很少考慮蒸氣云爆炸的影響。目前應用較多的蒸氣云爆炸潛在影響半徑預測模型包括TNT當量模型、TNO多能法、Baker-Strehlow模型等^[18-20]，但以上模型所需參數較多，計算過程較為復雜，目前并沒有簡化模型來計算蒸氣云爆炸潛在影響半徑，只能依賴專業軟件完成計算。ASME B31.8S中的簡化公式也只針對噴射火計算潛在影響半徑，并沒有考慮蒸氣云爆炸沖擊波的影響。

3  實例對比分析

應用油氣管道失效后果定量評價軟件RiskInsight對某輸氣管道破裂后發生噴射火及蒸氣云爆炸的影響半徑進行計算，并與ASME B31.8S簡化公式計算結果進行對比（見表 1、2）。

該管道管徑為1 016 mm，運行壓力為8 MPa，壁厚為12 mm，本次模擬泄漏點距離上游閥室9.1 km，距離下游閥室6.7 km，模擬管段長度約為17.35 km。選取風速2.6 m/s，大氣穩定度D，作為氣象條件計算參數，模擬工況為管道發生破裂時的火災爆炸潛在影響半徑。

 

表1  管道破裂時火災熱輻射潛在影響半徑

 

表 2   管道破裂時蒸氣云爆炸沖擊波潛在影響半徑

 

對比結果顯示：ASME B31.8S簡化公式只能計算輸氣管道發生破裂時人員1%概率死亡的潛在影響半徑，且其計算結果較RiskInsight軟件小。同時通過RiskInsight軟件對管道破裂后的蒸氣云爆炸沖擊波潛在影響半徑進行計算，發現蒸氣云爆炸沖擊波的潛在影響半徑要比噴射火熱輻射大。所以在確定輸氣管道安全距離時，還需要根據周邊氣象及地形條件，一旦有可能形成蒸氣云爆炸，需要考慮其可能對周邊人員的影響。

4  結論

綜合上述分析，GB 32167-2015《油氣管道完整性管理規范》中給出的輸氣管道潛在影響半徑的計算公式是進行了大量簡化的，在泄漏衰減因子、泄漏系數、熱輻射計算模型、火災熱輻射閾值等方面的取值，都會導致與真實事故影響半徑的偏差。管道管理者仍可以采用該公式進行快速的計算管道潛在影響半徑，但需要注意該公式的前提假設，計算結果只能作為初步的估算結果，并保守使用。

參考文獻：

[1]STEPHENS M J，LEEWIK，MOOREDK. A model for sizing high consequence areas associated with natural gas pipelines[C]. Alberta：The 4^thInternational Pipelines Conference，2002：759-767.

[2] American Society of Mechanical Engineers. Managing System Integrity of Gas Pipelines: ASME B31.8S-2012 [S]. New York：ASME B 31Committee，2012.

[3] 中國石油化工股份有限公司青島安全工程研究院．石化裝置定量風險評估指南[M]．北京：中國石化出版社，2007：56-98．

 [4] 賈偉，朱建新，高增梁，等. 區域定量風險評價方法及其在化工園區中的運用[J]. 中國安全科學學報，2009，19（5）：140-146.

[5] 王新，張華兵. 油氣管道失效后果定量評價軟件研發[J]. 煤氣與熱力，2017.

[6] 谷志宇，董紹華，牛景弘，等．天然氣管道泄漏后果影響區域的計算[J]．油氣儲運，2013，32（1）：

[7]Bilo M, Kinsman P R. Thermal radiation criteria used in pipeline riskassessment[J]. Pipes & pipelines international，1997， 42（6）：17-25.

[8] TNO. Safety study on the transportationof natural gas and LPG byUnderground Pipeline in the Netherlands [R]. Netherlands organization for Applied Scientific Reserch，1982.

[9] Hill R T，Catmur J R. Risks from hazardous pipelines in the United Kingdom[R]. HSE CONTRACT RESEARCH REPORT，1994.

[10]Dong Y H，Gao H L，Zhou J E. Mathematical modeling of gas release through holes in pipelines[J]. Chemical Engineering Journal，2003（92）：237–241.

[11]何沫，廖柯熹. 輸氣管道潛在影響區模型關鍵參數取值討論[J]. 當代化工，2015，44（3）：608-611.

[12] AdvisoryCouncilon Dangerous Substances.Guidelines for quantitativeriskassessment(Purple Book)[M].The Netherlands，2005.

[13] 霍春勇，董玉華，余大濤，等. 長輸管線氣體泄漏率的計算方法研究[J]. 石油學報，2004，25(1)：101-105.

[14] 劉俊娥. 城市燃氣管道噴射火事故后果分析[J].河北工程大學學報：自然科學版，2007，24（4）：53-56.

[15] 王兆芹，馮文興，程五一. 高壓輸氣管道噴射火幾何尺寸和危險半徑的研究[J].安全與環境工程，2009，16（5）：108-110.

[16] American  Petroleum  Institute. Risk based Inspection Technology：API 581-2008[S]. Washington：American Petroleum Institute，2008．

[17] 王小完，馬驥，駱正山．基于天然氣管線泄漏蒸汽云爆炸危害分析[J]．災害學，2013，28（3）：16-19．

[18] 張網，呂東，王婕. 蒸氣云爆炸后果預測模型的比較研究[J]. 工業安全與環保，2010，36（4）：48-52.

[19] Center for Chemical Process Safety. Guidelines for ConsequenceAnalysis of ChemicalReleases [M]. American Institute of Chemical Engineers，New York：1999.

[20] 張華兵．基于失效庫的在役天然氣長輸管道定量風險評價技術研究[D]．北京：中國地質大學，2013：53-62．

 

作者：王新， 1984年生，畢業于中國科學技術大學安全工程及技術專業，碩士，工程師，目前在中國石油管道科技研究中心從事管道風險評價相關工作。

 

《管道保護》2017年第5期（總第36期）